AbstractIf you can look into the seeds of time, and say which grains will grow and which will not, speak then to me who neither beg nor fear your favour nor your hate.
William Shakespeare (~1564–1616)
Poet and playwright
Increasingly, our critical infrastructure is managed and controlled by computers and the information networks that connect them. Cyber-terrorists and other malicious actors understand the economic and social impact that a successful attack on these systems could have. While it is imperative that we defend against such attacks, it is equally imperative that we realize how best to react to them. This article presents the strongest-path method of analyzing all potential pathways of exposure to risk – no matter how indirect or circuitous they may be – in a network model of infrastructure and operations. The method makes direct use of expert knowledge about entities and dependency relationships without the need for any simulation or any other models. By using path analysis in a directed graph model of critical infrastructure, planners can model and assess the effects of a potential attack and develop resilient responses.
Introduction
The complex connectedness of infrastructure, processes, commodities, and services in our society gives rise to risk. Failure of any particular system or service can cause far-reaching harm propagated through networks of other systems. A striking example is the electrical power failure that crippled much of Ontario and the northeastern United States in August 2003. The triggering event was a software bug in a control room system in Ohio, and it allowed a disastrous power surge to cascade through the power distribution grid. In addition to the usual direct effects of a power failure, unanticipated indirect effects were also experienced in the telecommunications, food, and transportation sectors. For example, in the Detroit area, residents lost water pressure because of failed pumps in the water supply system. However, the lack of pressure in the system resulted in potential contamination of the drinking water, which resulted in a “boil water advisory” after the pressure was restored.
In order to safeguard society, we need to connect with our connectedness. Models are needed to prepare for all recognized risks so that actions can be taken to make our communities, businesses, governments and environments as resilient as possible.
Typically, risk analysis of systems with complex dependency relationships is carried out by means of simulation. (A constructive simulation is a computer program in which software components mimic the behavior of infrastructure entities. Systems dynamics (http://en.wikipedia.org/wiki/System_dynamics) provides a framework and tools for building a constructive simulation. However, such models are governed by mathematical equations that are difficult to calibrate against the real world. Extensive data gathering and complex computer programming are required to create a useful model. Consequently, simulation models are time-consuming and costly to develop.
This article presents a technique, called the strongest-path method, which has been evolving since preparations began to solve the Year 2000 problem, or “Y2K”. The paradigm, together with calculation tools and graphical output features, has been implemented under the trade name RiskOutLook as java-based software available exclusively from Deep Logic Solutions Inc.
The strongest-path method fathoms all potential pathways of exposure to risk – no matter how indirect or circuitous they may be – in a network model of infrastructure and operations. The method makes direct use of expert knowledge about entities and dependency relationships without the need for any simulation or any other models. It can, however, incorporate results from simulation and other models if any are available.
This article will present the strongest-path method as a modelling paradigm, founded on risk analysis, that makes use of path analysis in a network representation of the entities and relationships in the environment of interest. The article starts with a description of the fundamental ideas in the paradigm. Next, it provides background information on risk analysis and path analysis in representations of networks in order to develop the tools for risk analysis used in the strongest-path method. Next, an example problem is used to demonstrate a practical use of the method and tools. Finally, the implications of this approach for planners and managers are discussed and conclusions are provided.
The Modelling Paradigm
Modern society can be viewed as a collection of networks that overlap and interact with each other. There are transportation networks, communications networks, energy networks, supply chains, distribution networks, social networks, cyber networks, and so on. In both private enterprise and public service, from the national level down to the local community level, planners typically divide their planning domain into coherent subsets called sectors. For example, at the provincial emergency planning level in Ontario, Canada, the following sectors are defined:
- Food
- Water
- Electricity
- Communications
- Healthcare
- Finance
- Natural Gas
- Oil
- Transportation
- Government
- Public Safety and Security
Each sector takes inputs from other sectors and, by means of its own actors and activities, produces outputs that are in turn taken as inputs by other sectors. As well, there are internal and external controls and regulations that govern the activities of any sector along with monitoring and verification agents who oversee the activities and processes.
Planners describe their domains in terms of the actors, actions, controls, agents, inputs, and outputs that exist in their sector. For purposes of risk analysis, distinct and significant actors that exist in a sector will be referred to as entities. An interaction between two entities will be referred to as a relationship. By using a mathematical object known as a directed graph, RiskOutLook creates a network model of entities and relationships that embodies the planner’s domain. Entities will be modelled as nodes in the graph and relationships will be modelled as links in the graph, which are called edges. Because all of the edges have a direction from one entity to another, the graph is a directed graph.
A dependency relationship is a special kind of relationship in which there is a transaction between two entities. The transaction can be physical (e.g., electricity or water) or non-physical (e.g., data or instructions). The risks in our society that result from connectedness can be characterized as stemming from dependency relationships. The strength of a relationship is measured by a weight called the degree of dependence.
Direct dependency relationships are well understood by domain experts; indirect dependencies are more complex. Modelling and analysis is needed to verify or correct intuition and to synthesize expert knowledge into a comprehensive assessment of the effects of direct and indirect dependencies and their associated risks.
Risk and Dependency Analysis
For purposes of infrastructure analysis, risk is the possibility of loss (Rowe, 1988). The strongest-path method describes loss using two dimensions: i) degree of impact and ii) likelihood of occurrence. The method then proceeds to aggregate assessments of cumulative impact resulting from multiple pathways of exposure to loss through pathways in the network model.
Estimates of likelihood of occurrence can be made in terms of “degree of belief” or “expert judgment”. For the purposes of modelling infrastructure, experience has shown that a scale of high, medium, and low is sufficient. High-likelihood events are deemed to have more than an 80% likelihood of occurrence and low-likelihood events are deemed to have less than 20% likelihood of occurrence during the time interval under consideration; all other events therefore have a medium likelihood of occurrence. More complex models can be created for situations that evolve over multiple time intervals.
An infrastructure is said to “fail” if it falls below a threshold level of its expected or required outputs. From this definition, we develop the following criteria for degree of direct dependence:
- If failure of entity x inevitably leads to failure of entity y, then y has a high direct dependency on x, and conversely x has a high direct impact on y.
- If failure of entity x leads to degradation of entity y to the extent that y must enact a contingency plan or resort to alternate operating procedures in order to stay above the expected threshold, then y has a medium direct dependency on x and conversely x has a medium direct impact on y.
- If failure of entity x leads to significant degradation of entity y, but y can stay above its expected threshold without significantly changing its operating procedures, then y has a low direct dependency on x and conversely x has a low direct impact on y.
- If failure of entity x does not lead to significant degradation of entity y, then y has zero direct dependency on x, and conversely x has zero direct impact on y.
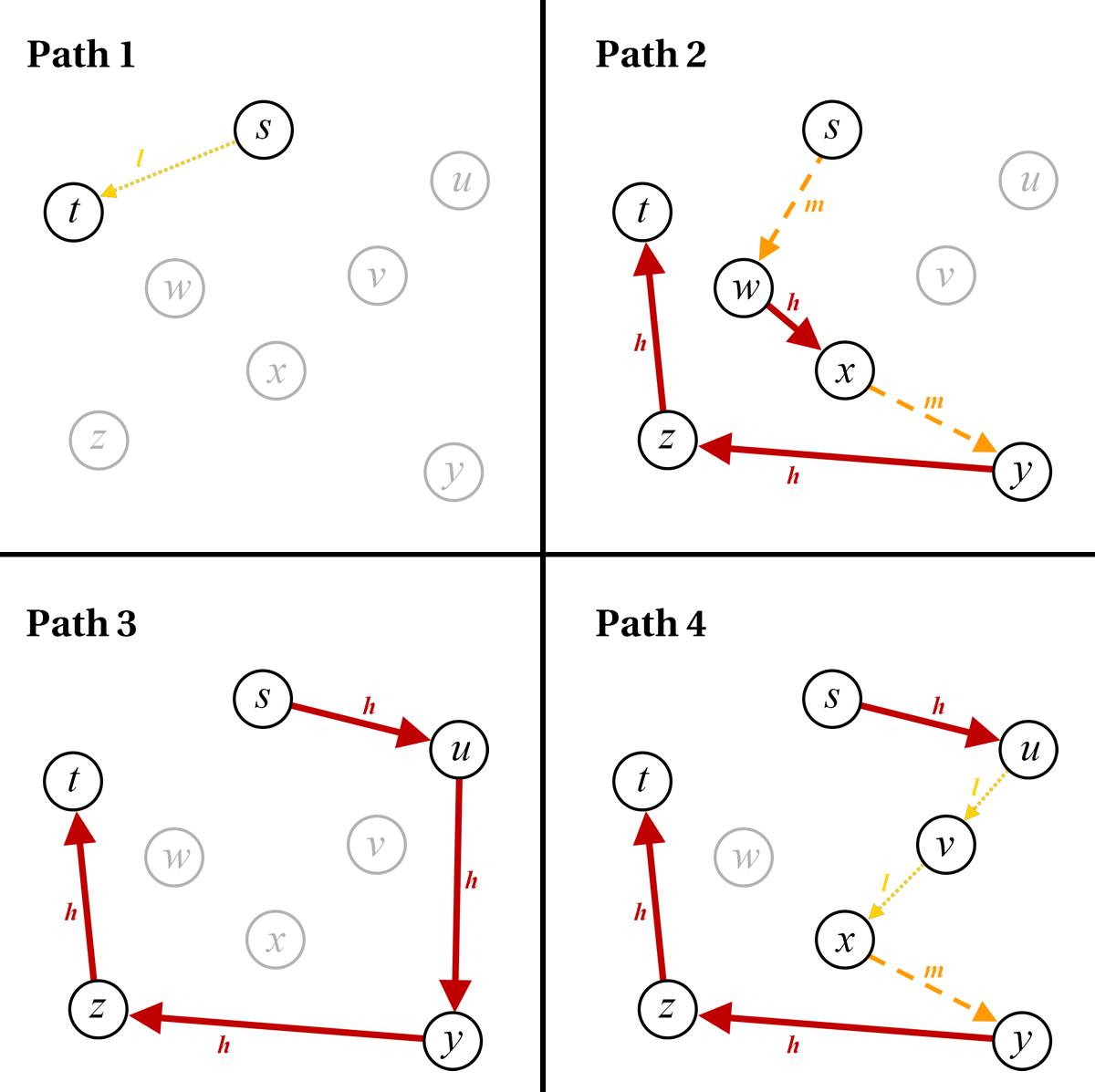
A directed path in a directed graph is a sequence of nodes with the property that each node in the sequence is connected to its successor by an edge. For example, in Figure 1, {s→w→x→y} is a directed path, whereas {s→w→x→v} is not, because {x→v} does not exist.
Figure 1. A directed graph with weighted edges (red/solid = high impact, orange/dashed = medium impact, yellow/dotted = low impact)
In order to derive a method for estimating the impact of every node in a graph on all nodes in the graph, path analysis is used. In particular, the analysis will be used to identify the paths of strongest impact, from any node x to any node y (including x itself). The paths of strongest impact, will be referred to as strongest paths. To visually indicate the strength of impact in a directed graph (e.g., Figure 1), the edges are coded as follows: red/solid for high impact, orange/dashed for medium impact, and yellow/dotted for low impact.
We have described the effect of a high direct impact event on a direct dependent. However, we also need to estimate the effect of a medium direct impact event and a low direct impact event on a direct dependent. There are two dimensions for this estimate: i) the degree of the triggering impact event and ii) the degree of the direct dependency relationship.
It is reasonable to expect that a strong triggering event will have little impact if the degree of dependence is low, whereas even a relatively weak triggering event will be felt if the degree of direct dependence is high. Thus, we estimate that the propagated impact can be no higher than the lesser of the triggering degree of impact and the degree of dependence. For example, according to this principle, a medium-degree triggering impact acting over a low-degree of direct dependence will cause a low impact because the degree of direct dependence is low, whereas, a medium-impact trigger acting over a high degree of direct dependence can cause a medium impact because of the high degree of direct dependence.
As we proceed along a path in Figure 1, our propagation rule compares the lowest-degree edge we have yet encountered with the degree of the next edge on the path and sets the triggering degree of impact to the lower value. Therefore, the indirect dependence of any node on any other node along a selected path is driven by the lowest-degree edge along that path. For example, consider the graph in Figure 1 and all paths connecting s to t. These four paths are shown in Figure 2 and can be described as follows:
- Path 1 = {s→t}
- Path 2 = {s→w→x→y→z→t}
- Path 3 = {s→u→v→x→y→z→t}
- Path 4 = {s→u→y→z→t}
Figure 2. All paths connecting s to t in the graph shown in Figure 1
Using the propagation rule, we find that the impact of s on t from Path 1 is low by virtue of (s, t), the impact of s on t from path 2 is medium by virtue of (s, w) and (x, y), the impact of s on t from Path 3 is low by virtue of (u, v) and (v, x), and the impact of s on t is high from Path 4 by virtue of all of its edges being high degree. Therefore, the indirect dependence of t on s is high and the strongest path is Path 4.
Proceeding from the direct impact and likelihood of failure of each node coupled with the ability to measure the strongest path from one node to any other, we can calculate other useful metrics. For any nodes x and z in any directed graph we can calculate:
- Strongest-path impact of x on z: This is the strongest-path degree of dependence of z on x multiplied by the direct impact of x.
- Cumulative impact of x on z: This includes a term for every pathway that exists from x to z. Similar to the binomial probability function, this metric compounds the effects of all of the terms.
- Global impact of x on the entire graph: By “global”, we mean the impact of any node x on the entire graph. This metric is calculated using the impact x on every node z in the graph and summing the terms.
- Global vulnerability of x from the entire graph: The cumulative vulnerability of x from all nodes in the model is the binomial probability that a failure event of any node will cause x to fail.
- Risk index of x: The risk index of an entity is the product of the global impact of an entity times its global vulnerability. This metric provides a single score for comparing risk among all of the entities in a model.
Finally, we describe how to find the strongest-path degree of dependence between all pairs of nodes. By adapting any “shortest path” algorithm we can find a strongest path from any node x to any node z as follows:
- Within the graph, remove all edges except for those of high degree.
- If the shortest path from x to z exists, then it is a strongest path and z has high dependence on x.
- Otherwise, put the medium-degree edges back into the graph.
- If the shortest path from x to z exists, then it is a strongest path and z has medium dependence on x.
- Otherwise, put the low-degree edges back into the graph.
- If the shortest path from x to z exists, then it is a strongest path and z has low dependence on x.
- Otherwise, z has zero dependence on x.
A Practical Application of the Method
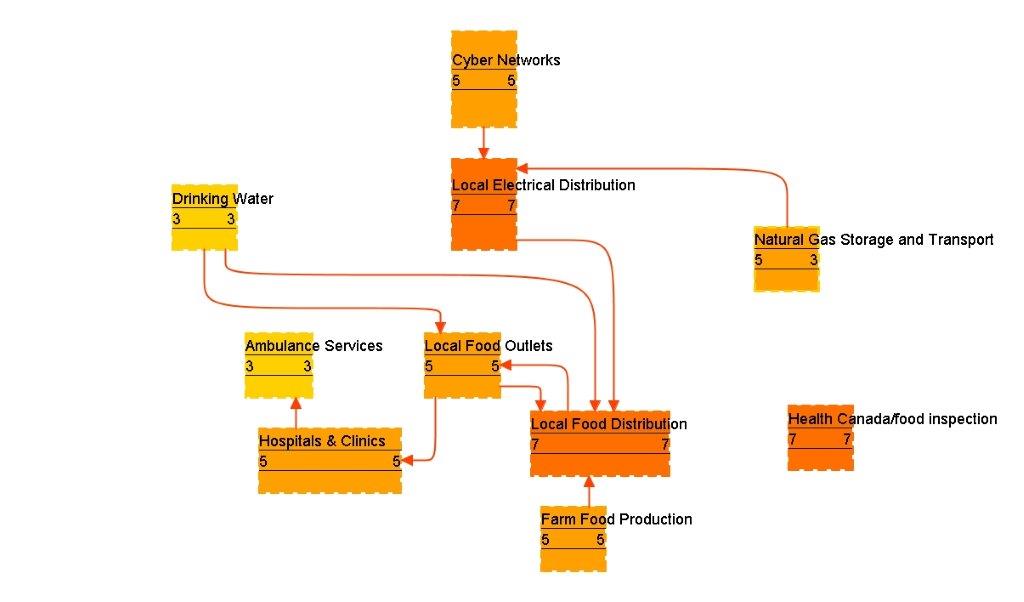
In this section, we use an example network model to illustrate the practical use of the strongest-path method. The example model, shown in Figure 3, is a small infrastructure model with 10 entities: Drinking Water, Local Electrical Distribution, Natural Gas Storage and Transport, Ambulance Services, Local Food Outlets, Local Food Distribution, Farm Food Production, Health Canada/Food Inspection, Hospitals & Clinics, and Cyber Networks.
For each of these entities, the degree of impact has been assessed, as indicated by the number on the left side of each node in Figure 3: high (score = 7, dark orange), medium (score = 5, orange), or low (score = 3, yellow). As well, the likelihood of failure has been assessed for each entity, as indicated by the number on the right side of each node: high (score = 7, dark orange border), medium (score = 5, orange border), or low (score = 3, yellow border).
Figure 3. A small infrastructure model
There are 30 direct-dependency relationships that have been scored high (score = 9, red edges), medium (score = 5, orange edges), and low (score = 3, yellow edges). All entities except Local Electrical Distribution have been assessed as having medium dependence on Cyber Networks. Local Electrical Distribution, however, has been scored as having high dependence on Cyber Networks.
After path analysis is carried out and scores for global impact and global vulnerability are computed, a histogram of the risk indices can be created, as shown in Figure 4. The bars represent risk-index scores arranged from the lowest score to highest score, from left to right. The highest-risk entity in the model is Local Electrical Distribution. The second-highest entity is Local Food Distribution. At medium risk are three entities: Health Canada/Food Inspection, Local Food Outlets, and Cyber Networks. The remaining entities are of relatively low risk.
Figure 4. Histogram of the risk indices for the model shown in Figure 3
Even though Cyber Networks is assessed as medium risk in the model, we can still assess all consequent impact were it to fail. Figure 5 shows the sub-network of high-dependency relationships in the model.
Figure 5. High-dependency relationships for the example model shown in Figure 3
From this sub-network, we can isolate the paths of high impact emanating out of the Cyber Networks entity, as depicted in Figure 6.
Figure 6. Paths of high impact from the Cyber Networks entity for the model shown in Figure 3
Although only Local Electrical Distribution has a high direct dependence on Cyber Networks, Figure 6 shows that Local Food Distribution, Local Food Outlets, Hospitals & Clinics, and Ambulance Services would all fail if Cyber Networks were to fail.
Discussion
The strongest-path method provides a tool for assessing and prioritizing risk. The risk index provides a global measure of risk for every entity in a model. This depiction of risk is of strategic value to decision makers in that it gives them a strategic prioritization of every entity.
Moreover, with the strongest-path method, the global impact and global vulnerability of every entity in a model is assessed so that a separate prioritization – based on either impact or vulnerability – is available to decision makers. Thus, any scenario of high impact can be identified, no matter how unlikely it is to occur. Conversely, possible situations of triggering events for unlikely scenarios can be identified from the path analysis.
With the strongest-path method, the influence of every node on every other node in a model is assessed. Consequently, decision makers can make plans based on identified pathways of exposure to risk. Risk-mitigation plans and contingency plans can take into consideration chains of events that might otherwise have gone unnoticed.
A model based on the strongest-path method can be made as detailed as required for the decision-making requirements of the planners or managers who will use it. Entities should embody the level of detail that is significant in the environment of interest. For example, a cyber network might be modelled at the level of individual servers and computers together with the direct connections that link them together. This model might also include entities and relationships that model power sources and the distribution of power.
In situations where entities and relationships change over time, a time-oriented model can be built using time-intervals that represent periods when changes do not occur among the entities and relationships. For example, consider a hospital that has a backup power generator with 36 hours of fuel to sustain it during a power failure. At t=0, the hospital has medium dependence on local power distribution because of its backup system. Once the power failure starts, it has high dependence on its backup generator until t=36 hours. By that time, it must have acquired more fuel or it must shut down, and it is deemed to have failed if there is low likelihood of having fuel delivered by that time. Any entities with high dependence on that hospital will also fail at t=36 hours.
Conclusion
The strongest-path method is a paradigm for modelling infrastructure risk using a directed graph. Models are constructed from entities that are assessed with a degree of impact and a likelihood of failure together with dependency relationships between the entities that are scored for degree of dependence according to well defined criteria.
The paradigm allows the knowledge of experts to be used for infrastructure risk analysis. Results from other analytical models, such as simulations, can also be included in a model. As a result of performing the path analysis, such models reveal the potential consequences of the failure of any entity on all of the others. This enables contingency planners to anticipate all outcomes in any infrastructure damage scenario.
The strongest-path method and the RiskOutLook software are currently being used by Emergency Management Ontario to manage risks in critical infrastructure. The provinces of New Brunswick and Saskatchewan will soon begin projects to build similar infrastructure models.
Keywords: critical infrastructure, cybersecurity, directed graph, modelling, path analysis, risk analysis, simulation, strongest-path method